Чтобы избежать проскальзывания и сохранить постоянное значение передаточного числа во время работы, рабочие поверхности колес снабжаются выступами, т. е. зубьями определенного профиля. Цилиндры с такими зубьями называются цилиндрическими зубчатыми колесами (рис. 3).
 |
Если коническую поверхность снабдить зубьями, то получится коническое зубча-тоо колесо 4 (рис. 3). Как и цилиндрические, конические колеса изготовляются с прямыми, косыми и шевронными зубьями. Рис. 3. Зубчатая передача. 1 — пара цилиндрических колес, 2 — цилиндрические колеса внутреннего зацеплении, з — цилиндрические колеса с паразитным средним колесом, 4 — конические зубчатые колеса, 5 — сложная последовательная передача зубчатых колес. |
Профили зубьев цилиндрических колес образуются (ограничиваются) эвольвентной поверхностью (рис. 4). На зубчатых колесах различают три окружности. Начальной окружностью называется условная окружность, по которой колеса, находящиеся в зацеплении, как бы катятся в процессе работы одно по другому. Окружность выступов De является наибольшим размером колеса по диаметру.
 |
Окружность впадин Di проходит но основанию зубьев. Начальная окружность d обозначается штрих-пунктирной линией, являющейся одновременно делительной окружностью при нарезании зубьев колеса, и делит зуб по высоте на две части. Верхнюю часть h1 называют головкой зуба, а нижнюю h2 — ножкой. Полная высота зуба составляет h = h1 + h2. Рис. 4. Основные параметры зубчатой передачи. |
Размер зуба S по начальной окружности называют толщиной зуба, а расстояние S0, измеренное по дуге начальной окружности, — шириной впадины. Сумма S + S0 = t — шаг зацепления. В зубчатых зацеплениях зависимость между шагом числом зубьев z и диаметром начальной окружности d выражают формулой:
d = t/π z
Отношение шага t к числу π называется модулем зацепления, т. е. t/π = m, и тогда диаметр начальной окружности выразится так: d = mz. В прямозубых колесах высота головки зуба h1 = m, высота ножки h2 = 1,2 т.
Если требуется, чтобы два параллельных вала вращались в противоположные стороны, то на эти валы устанавливаются колеса 1 (рис. 3) с внешним зацеплепием; при необходимости вращения обоих валов в одну и ту же сторону включается промежуточное 3 (паразитное) колесо или применяются, если допускает конструкция, колеса внутреннего зацепления 2. Передаточное число для одной пары шестерен определяется как отношение числа зубьев шестерен или диаметров начальных окружностей:

Если число оборотов (n1) ведущей шестерни разделить на передаточное число, то получим число оборотов ведомой шестерни, т. е.

Пример 1. Ведущее зубчатое колесо имеет z1 = 19, вращается со скоростью n1 = 80 об/мин, ведомое зубчатое колесо имеет z2 = 28. Определить число оборотов в миyуту ведомого колеса.

Если передачу вращения от одного вала к другому невозможно осуществить одной парой зубчатых колес, то принимают сложную передачу 5 (рис. 3) с одним или несколькими промежуточными валами. В подобных рядовых соединениях передаточное число i равно частному от деления произведения числа зубьев ведомых шестерен на произведение зубьев ведущих шестерен:

где нечетпые индексы при числах зубьев z относятся к ведущим шестерням, четные — к ведомым.
Пример 2. В сложной последовательной передаче 5 (рис. 3), где: z1 = 16; z2 = 30; z3 = 15 и z4 = 24, передаточпое число будет:

Если ведущей шестерней в сложной передаче 5 является z4, то передача будет ускорительпой, т. е.
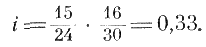
При определении передаточного числа последовательно-рядового зацепления промежуточные колеса не принимаются в расчет, так как они изменяют только направление вращения, а не число оборотов ведомого колеса 3 (рис. 3).
Кроме рядового последовательного соединения шестерен, применяются и другие виды сложных соединений.
Передача между параллельными валами осуществляется цилиндрическими зубчатыми колесами; при пересекающихся валах применяются конические колеса 4 (рис. 3).

